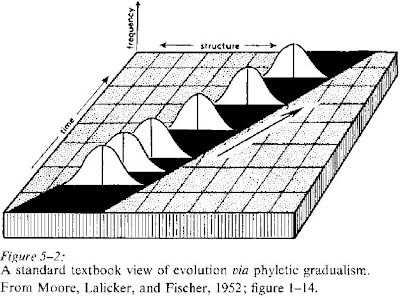
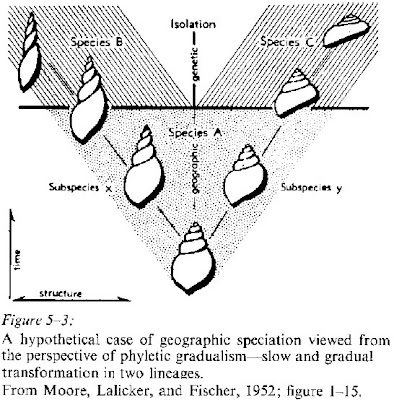
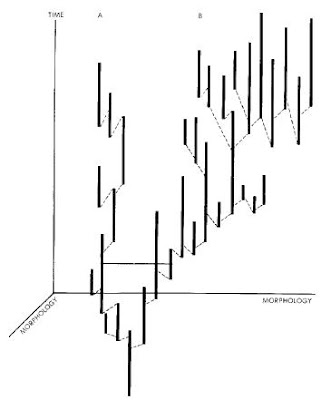
From NatureNews: Brown pledges to protect science during downturn.
From NatureNews: Brown pledges to protect science during downturn.British Prime Minister Gordon Brown said he would not let science "become a victim of the recession" in a speech today at the University of Oxford.Meanwhile, Stephen Harper and the Conservative Party are cutting the budgets of the major granting agencies in Canada.
Speaking to an invited audience, Brown said he would defend investment in science by maintaining the ring fence around the science budget, so that it cannot be raided to prop up other areas competing for public funds such as the health service and industry.
He signalled his aim for Britain to move away from an economy "heavily centred" on financial services and towards one focused on science.
....
Responding to Brown's speech, Nick Dusic, director of the Campaign for Science & Engineering in the UK (CaSE), a London-based lobby group says, "The prime minister is absolutely right that now is the time to show the world the UK is the place to do science. Unfortunately he needed to go further today in his commitments because other countries are raising the bar by making science and engineering central to their economic recovery."
Dusic added that just maintaining current spending commitments will mean that Britain loses ground against countries, like the United States, that are giving science a huge boost within their stimulus packages.
How stupid is that?